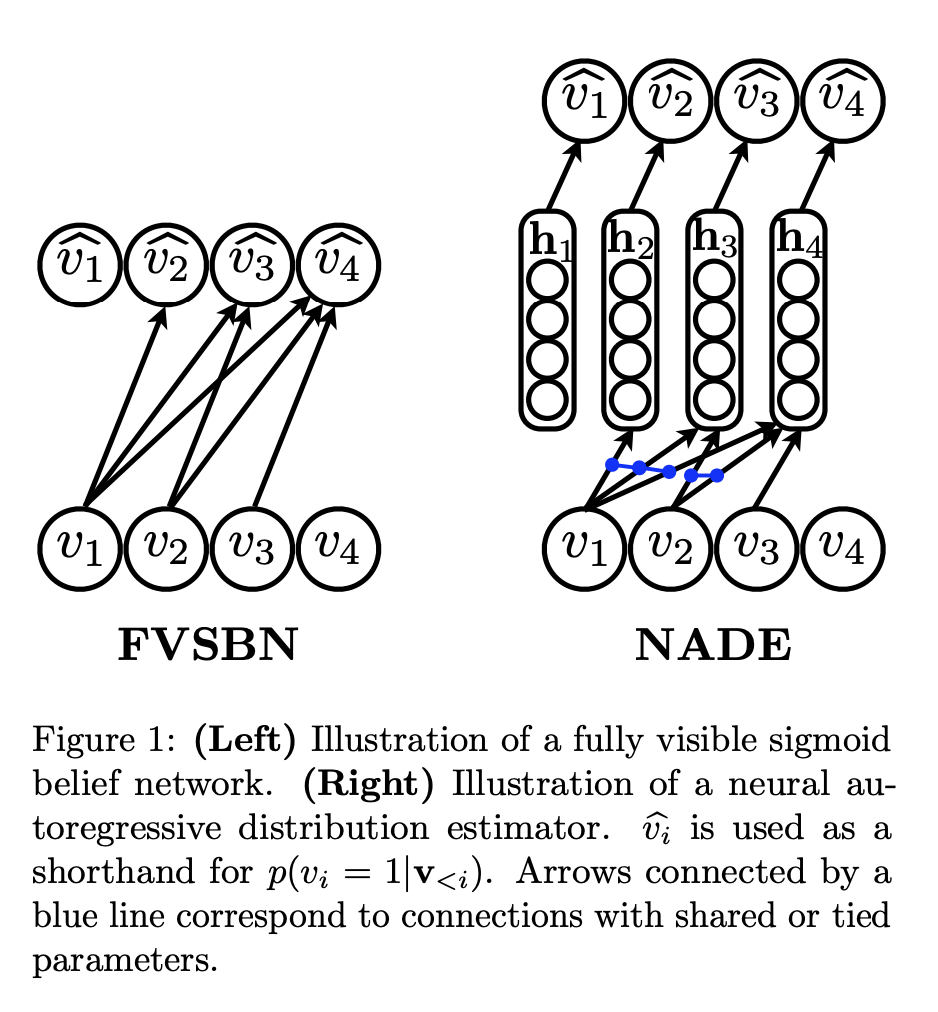
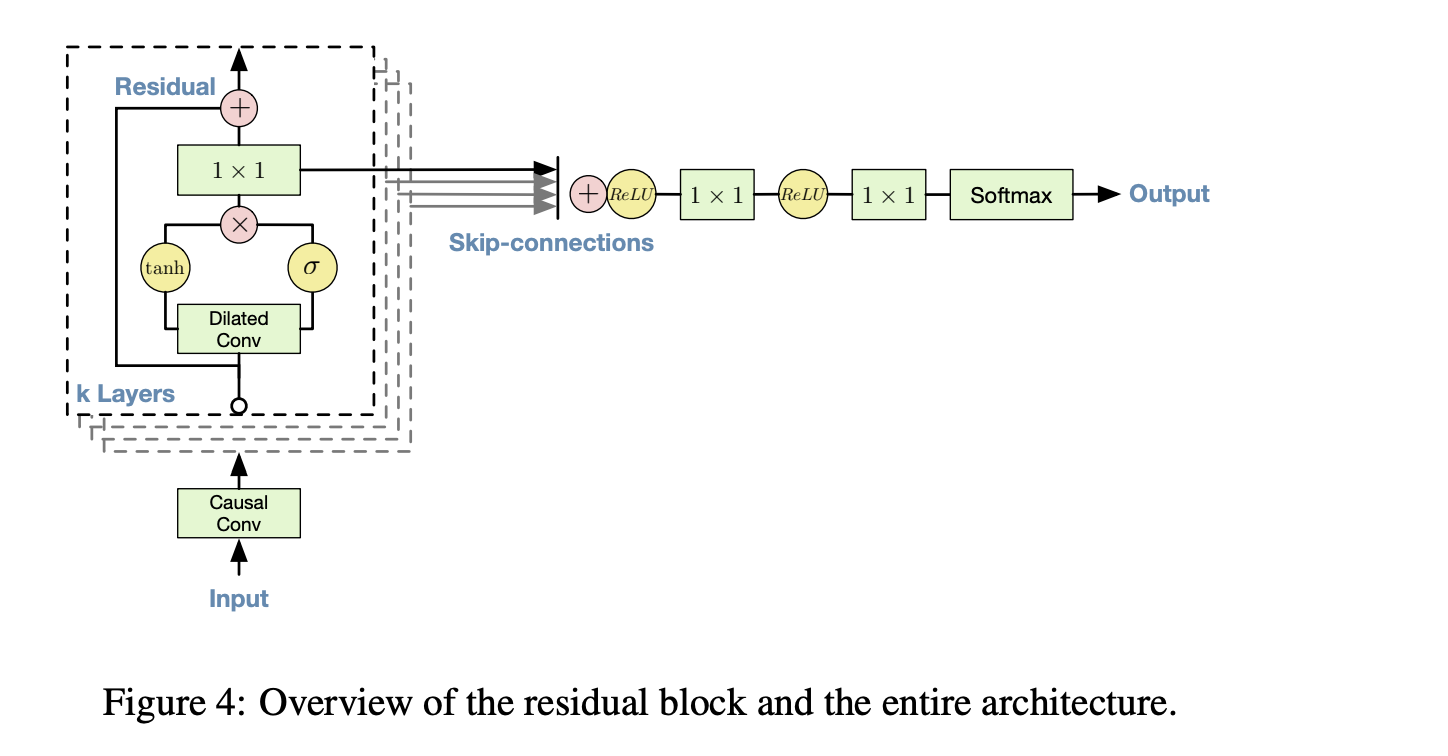
Generating speech with Wavenet (conditioning)¶
WaveNet architecture has been used for Text-to-Speech generation.
In order to condition the generation on text, the conditioning has been introduced into the architecture.
It is achieved by upsampling such local features to the level and using inside the gating mechanism
Given $h_t$, possibly with a lower sampling frequency than the audio signal, e.g. linguistic features in a Text-to-Speech (TTS) model.
This time series is first transformed using a transposed convolutional network (learned upsampling) that maps it to a new time series $\mathbf{y}=f(\mathbf{h})$ with the same resolution as the audio signal,
which is then used in the activation unit as follows:
$$
\mathbf{z}=\tanh \left(W_{f, k} * \mathbf{x}+V_{f, k} * \mathbf{y}\right) \odot \sigma\left(W_{g, k} * \mathbf{x}+V_{g, k} * \mathbf{y}\right)
$$
Note the gating mechanism again (actually, quite powerful idea).