Lecture 9: Training large models

Previous lecture: General tricks for efficient training:

• Data augmentation (AutoAugment, RandAugment)
• Label smoothing (CutMix, MixUp, ...)
• Self-training (NoisyStudent, PseudoMetaLabels)
• Gradient clipping
• multi-precision training
• Software (ML composer)

Current lecture: Training of large deep models

• checkpointing
• offloading
• efficient communications
• low-precision training.

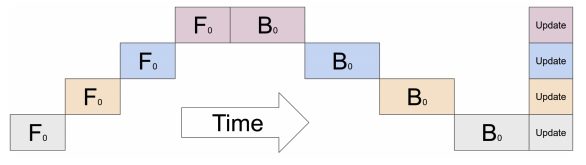
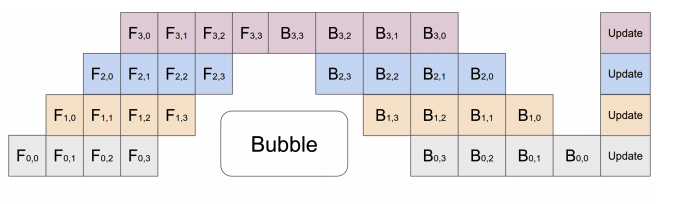
Models are getting larger and larger, and requiring larger compute

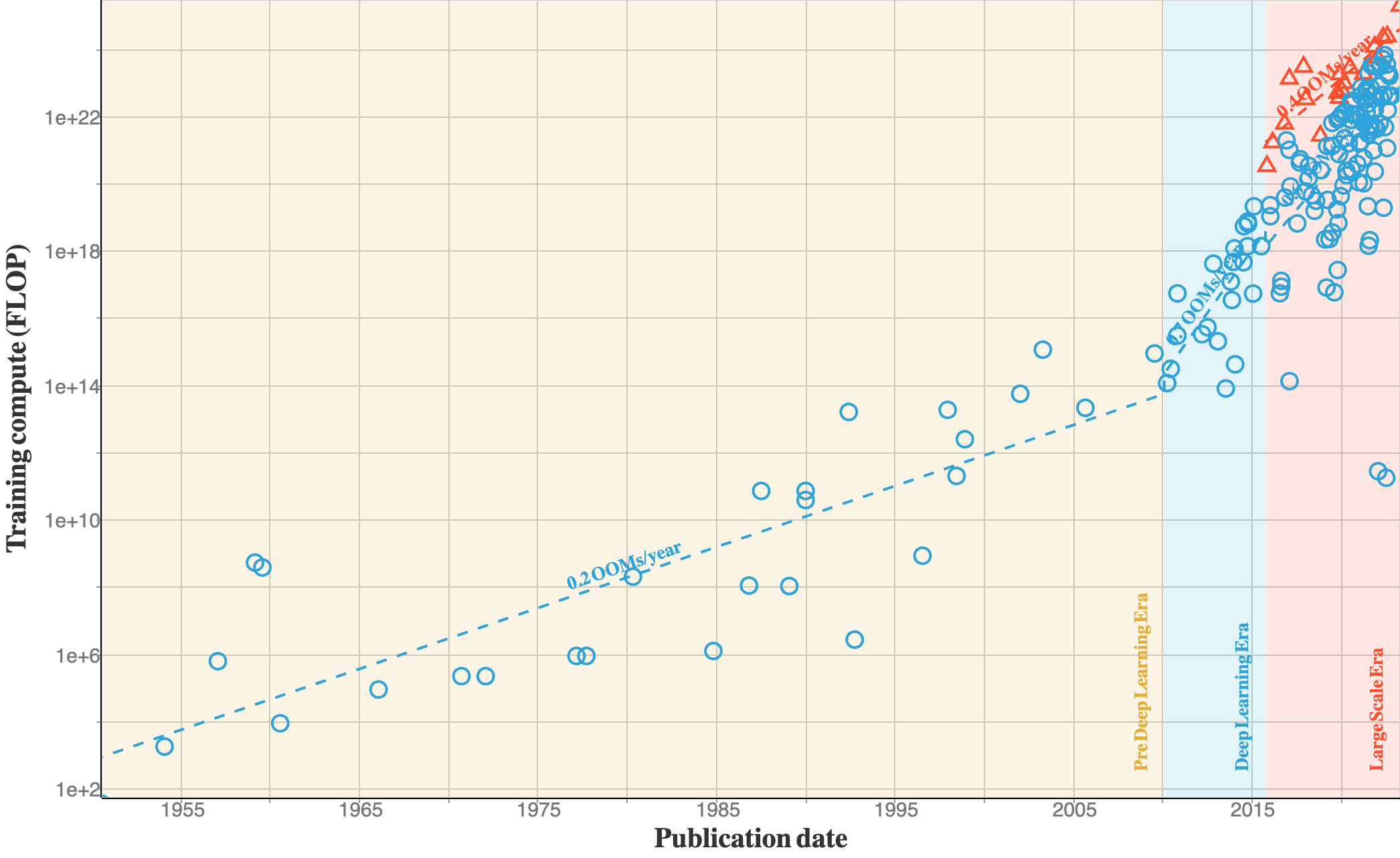
Also, the computational trends are quite interesting, and can be splitted into 3 different eras.

The analysis is taken from here

1. The Pre-Deep Learning Era: Prior to Deep Learning, training compute approximately follows Moore’s Law, with a doubling time of approximately every 20 months.

2. The Deep Learning Era: This starts somewhere between 2010 and 2012, and displays a doubling time of approximately 6 months.

3. The Large-Scale Era: Arguably, a separate trend of of models breaks off the main trend between 2015 and 2016. These systems are characteristic in that they are run by large corporations, and use training compute 2-3 orders of magnitude larger than systems that follow the Deep Learning Era trend in the same year. Interestingly, the growth of compute in these Large-Scale models seems slower, with a doubling time of about 10 months.

Why larger models

• Large models show better performance (GPT-1, GPT-2, GPT-3)
• Single models for multimodal data

Memory constraints when training large models

Large models do not fit to a GPU memory;

A rule of thumb is that for M parameters we need 12M bytes

12 = 4 bytes x 3 optimizer states

Activations take (0.1 - 10) x number of parameters.

Without offloading/checkpointing maximum is 2 billion on a V100 GPU.

Checkpointing

For a backward pass, we need to store activations! They consume 0.1 - 10x of the memory of the model (depending on the batch size)

Where the memory goes

Unfortunately, this is the intrinsic property of the backward pass: we need to store intermediate computations.

There were recent papers on 'forward propagation' but they just implement random search.

https://arxiv.org/pdf/2202.08587.pdf

How we can reduce the memory?

Checkpointing aims at saving part of the activations and recomputing the rest.

It add computations but it reduces the amount of time we need.

This technique is called rematerialization or activation checkpointing.

Checkpointing

How to do the optimal checkointing? I.e. which activations to save or load?

1. For a general computational graph, this is an NP-complete problem.
2. For linear graph we have dynamical programming.
3. Efficient realization is available in the ROTOR package.

We are now trying to do the same thing for transformers, but it is much more complicated.

Another memory reduction technique: gradient accumulation

Standard SGD: make a gradient for a batch, and update the weights.

If the batch is large, the intermediate computations will not fit into the memory.

Instead, we do the cycle of the batch and sum the result. Memory consumption is much smaller, the result is the same.

DeepSpeed framework

One of the most popular and efficient frameworks for training large models is DeepSpeed.

https://github.com/microsoft/DeepSpeed

For example, Zero-Offload part implements offloading: parts of the models and part of the data is stored in the CPU memory, which is typically much larger, than the GPU memory.

Optimal offloading strategy is again an NP-complete thing.

What else can we do?

Besides rematerialization and offloading, we can you good old paralllel computations.

We split the work between different GPUs.

There are different types of parallelism:

1. Data parallelism: split the input batch into sub-batches
2. Model parallelism: split the parameters of the model between different computational nodes
3. Pipeline parallelism: minimize communication in forward & backward passes
4. Tensor parallelism: split the feature dimension between different GPUs

Data parallelism

The classical approach, implemented in software, is data parallelism

Each computational unit holds a copy of the model, processes its own batch and aggregates the gradients.

This is equivalent to large batch;

It also requires scatter-gather operation.

What do you think are main challenges in data parallelism?

Challenges in data parallelism

There are two main challenges in data parallelism.

1. Total communication costs

2. The larger batch can lead to worser convergence of SGD!! (Lets discuss why)

Large-batch training

Large batch training is solved by learning rate schedule. Although not used too much, optimizers such as LARS and LAMB

Training BERT in 76 minutes

Training BERT in 76 minutes

Communication in data parallelism

We need to send a lot of data: we need to have $P$ copies of the model, so quite a lot of computations.

How we can parallelise the computations instead?

As usual in parallel computations, we need to think about good ways of splitting the data.

ZERO (DeepSpeed)

The DeepSpeed frameworks implements different splitting of the data between computational nodes.

The weights of the model, the gradients and the optimizer parameters (do not need to be forgotten) can be split among all processors.

Then, (non-trivial) communication scheme has to be derived.

Pipeline parallelism

One of the challenges is that in feedforward networks with the model weights split, the computations are sequential and difficult to parallelism.

Can you come with an idea how to do it?

Pipeline parallelism

The solution is known as pipeline parallelism and is again --- NP-complete for a general computational graph.

Many heuristics have been proposed, including PipeDream and GPipe.

A typical solutions involves splitting the mini-batch into micro-batches and inteleaving computations of the forward/backward pass with computations. An example solution is shown on the picture.

There are actually better solutions (and no optimal ones!)

Tensor parallelism

Finally, if the layers are very large,

one can start splitting single weights and parallelise them along different GPUs.

Believed to be last resort.

It can actually might not be true!

Other techniques for faster training

• Low-bit optimization
• Gradient compression

8-bit Adam

8-bit Adam paper showed that during Adam optimization we can store optimizer states within 8-bits.

This significantly reduces the amount of memory you need to use!

You can also use 8-bit matrix multiplication at inference

Gradient compression

One of the techniques used for DALLE-2 training was PowerSGD. They idea of power SGD is to consider the

$$N \times B$$

gradient matrix (which is split along the processors and has to be summed over $B$)

and approximate it with low-rank approximation.

The low-rank approximation is done by a simple block power iterations

One can also use 1-bit Adam/SGD by replacing the gradient by it sign. Then for communication you need 16-32 times less number of bits to store.

PowerSGD: algorithm

The algorithm has the following form:

Quantization of the gradients

One can also compute the gradient in backpropagation very inaccurately.

• We can compress the gradient for the activations
• We can compress the gradients for the linear layers
• We can compute the multi-head self-attention more efficiently.

Challenges in training large models

THe main challenge for training large models is that even for DeepSpeed

frameworks the efficiency is typically 30-60% of the peak performance.

Summary (1)

• Vanilla Pytorch/jax works badly with memory. Memory consumption could be reduced and large models fine-tuned even on the GPUs with large memory.
• Parallelism is not optimal, but data-parallelism & pipeline parallelism can be implemented and used.

Summary

• checkpointing
• offloading
• efficient communications
• low-precision training.

Next lecture: Contrastive learning / self-supervised learning

• What is contrastive learning
• Siamese Networks
• Triplet loss
• popular contrastive learning techniques